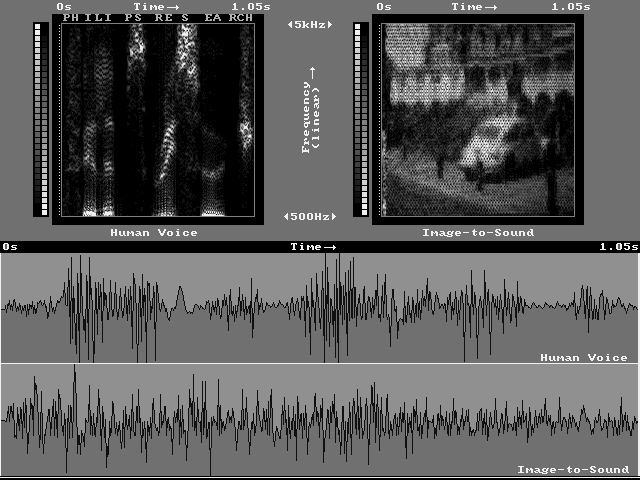
 Spectrogram and waveform for human voice and The vOICe auditory display |
A continuous wavelet transform (CWT) is a mathematical mapping that is in a number of ways similar to the classic Fourier transform: it is linear, invertible and orthogonal. However, contrary to the Fourier basis functions, the sines and cosines, which extend to infinity in time (hence are not localized in time), wavelet basis functions drop towards zero outside a finite domain. This allows for an effective localization in both time and frequency under the limitations imposed by the frequency-time uncertainty relation: the product of the uncertainty-in-frequency times the uncertainty-in-time will always be at least one over two pi (i.e., about 0.15915). That same relation lies at the heart of quantum mechanics, where the Heisenberg uncertainty relation applies to energy and time, because energy is, via Planck's constant, proportional to the frequency of probability waves. Anyway, because pure sines and cosines
|
Now wavelets have characteristic scales for localization in time and frequency ``built-in,'' sort of, but unlike sines and cosines, wavelets are not uniquely defined, and different definitions for these wave packets may be preferred for different situations. Some examples of established wavelet classes are the Daubechies wavelets, Lemarie wavelets, Haar wavelets, Gabor wavelets and spline wavelets. However, we will not go into the details of these here.
A major qualitative difference between wavelets and windowed (co)sines is that for a fixed-width time window the characteristic number of dominant oscillations in the windowed (co)sine would be linearly dependent on frequency (or rather on basis function count), while for wavelets the number of dominant oscillations tends to be approximately constant. Simply put, more periods of a (co)sine fit into a given time interval at higher frequencies, whereas the wavelet widens its own ``time interval'' (effective width) to keep the number of periods in this interval about constant. Of course, there is no basic reason why one could not apply this same trick of variable window widths to windowed (co)sines to get the kind of constant quality factor (constant-Q) analysis as offered by wavelets - for applications where this would be appropriate: just take the effective width of a time window for a sinusoid inversely proportional to its frequency.
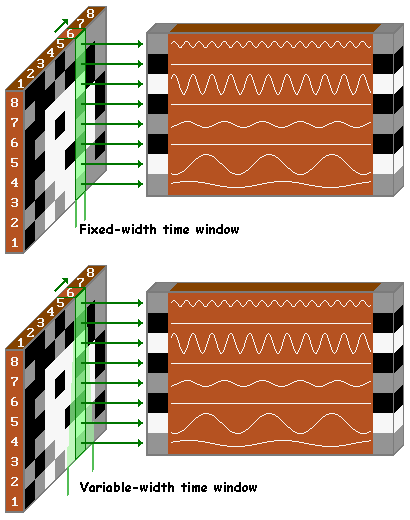 Consequently, unless the mathematical properties of having an exact lossless and/or orthogonal
mapping and its inverse reconstruction are considered essential, there is no really convincing
reason to use wavelets in sound synthesis and analysis. For instance, in
auditory perception almost nothing is exact,
even though the localization properties in time and frequency are very
important. There is also no reason why the resonance properties of the basilar membrane would
be best described using wavelets, since the constant-Q property approximates only part of the
membrane. Constant bandwith, as suited to fixed-width time windowing, better approximates the,
admittedly often less important, low-frequency part. Therefore, provided we consider using
variable-width time windows, it makes sense to give up on wavelets and their exact
orthogonality and other properties, in favour of alternative wave packets that may be better and
more easily ``tuned'' to (exploiting) the nonidealities of the human hearing system, just like it
can be useful to make an auditory spectrogram by logarithmic compression of the frequency scale to
reflect differences in frequency sensitivity along the auditory spectrum. Furthermore, the human
hearing system is known to be nonlinear in a number of ways, so even without knowing how to exploit
that one can argue that a linear mapping is most likely not going to be an optimal mapping for human
auditory scene analysis - although it may be quite good for most practical purposes. Alternatively, one
may prefer the windowed (co)sines because of their conceptual simplicity, flexibility in exloring
various time-frequency envelopes, and efficient implementation in software and hardware.
Consequently, unless the mathematical properties of having an exact lossless and/or orthogonal
mapping and its inverse reconstruction are considered essential, there is no really convincing
reason to use wavelets in sound synthesis and analysis. For instance, in
auditory perception almost nothing is exact,
even though the localization properties in time and frequency are very
important. There is also no reason why the resonance properties of the basilar membrane would
be best described using wavelets, since the constant-Q property approximates only part of the
membrane. Constant bandwith, as suited to fixed-width time windowing, better approximates the,
admittedly often less important, low-frequency part. Therefore, provided we consider using
variable-width time windows, it makes sense to give up on wavelets and their exact
orthogonality and other properties, in favour of alternative wave packets that may be better and
more easily ``tuned'' to (exploiting) the nonidealities of the human hearing system, just like it
can be useful to make an auditory spectrogram by logarithmic compression of the frequency scale to
reflect differences in frequency sensitivity along the auditory spectrum. Furthermore, the human
hearing system is known to be nonlinear in a number of ways, so even without knowing how to exploit
that one can argue that a linear mapping is most likely not going to be an optimal mapping for human
auditory scene analysis - although it may be quite good for most practical purposes. Alternatively, one
may prefer the windowed (co)sines because of their conceptual simplicity, flexibility in exloring
various time-frequency envelopes, and efficient implementation in software and hardware.
For reasons like these, The vOICe auditory display applies windowed (co)sines, rather than wavelets both in its real-time hardware, as well as in The vOICe Web App, in The vOICe for Windows, and in The vOICe for Android. The windowed (co)sines are here called ``voicels,'' because these little tonebursts act as the auditory counterparts of pixels. In the implementation of voicels, a choice was made for variable order B-spline time windows, because
References:
W. M. Coughran, E. Grosse and D. J. Rose, ``Variation Diminishing Splines in Simulation,''
SIAM J. Sci. Stat. Comput., Vol. 7, pp. 696-705, April 1986. This is an excellent
paper highlighting the merits of QVD splines for device modelling.
P.B.L. Meijer, ``Fast and Smooth Highly Nonlinear Table Models for Device Modeling,''
IEEE Transactions on Circuits and Systems, Vol. 37, pp. 335-346, March 1990.
This paper shows alternatives for tensor products of QVD splines for highly nonlinear
multivariate data modelling.
For more information on sonification (auralization) by The vOICe, visit The vOICe Home Page.
