Chapter 5
Conclusions
To quickly develop new CAD models for new devices, as well as to keep
up with the growing need to perform analogue and mixed-signal simulation of very large circuits,
new and more efficient modelling techniques are needed. Physical modelling and table modelling
are to a certain extent complementary, in the sense that table models can be very useful in case
the physical insight associated with physical models is offset by the long development time of
physical models. However, the use of table models has so far been restricted to delay-free
quasistatic modelling, which in practice meant that the main practical application was in
MOSFET modelling.
The fact that electronic circuits can usually be characterized as being complicated nonlinear
multidimensional dynamic systems makes it clear that the ultimate general solution in modelling
will not easily be uncovered—if it ever will. Therefore, the best one can do is try and devise
some of the missing links in the repertoire of modelling techniques, thus creating new
combinations of model and modelling properties to deal with certain classes of relevant
problems.
5.1 Summary
In the context of modelling for circuit simulation, it has been shown how ideas derived from, and
extending, neural network theory can lead to practical applications. For that purpose, new
feedforward neural network definitions have been introduced, in which the behaviour of
individual neurons is characterized by a suitably designed differential equation. This differential
equation includes a nonlinear function, for which appropriate choices had to be made to allow
for the accurate and efficient representation of the typical static nonlinear response of
semiconductor devices and circuits. The familiar logistic function lacks the common transition
between highly nonlinear and weakly nonlinear behaviour. Furthermore, desirable mathematical
properties like continuity, monotonicity, and stability played an important role in
the many considerations that finally led to the set of neural network definitions as
presented in this thesis. It has been shown that any quasistatic behaviour can up to
arbitrary precision be represented by these neural networks, in case there is only
one dc solution. In addition, any linear dynamic behaviour of lumped systems can
be covered exactly. Several relevant examples of nonlinear dynamic behaviour have
also been demonstrated to fit the mathematical structure of the neural networks,
although not all kinds of nonlinear dynamic behaviour are considered representable at
present.
The standard backpropagation theory for static nonlinear multidimensional behaviour in
feedforward neural networks has been extended to include the learning of dynamic response in
both time domain and frequency domain. An experimental software implementation has already
yielded a number of encouraging preliminary results. Furthermore, the neural modelling software
can, after the learning phase, automatically generate analogue behavioural macromodels and
equivalent subcircuits for use with circuit simulators like Pstar, Berkeley SPICE and Cadence
Spectre. The video filter example in section 4.2.6 has demonstrated that the new techniques can
lead to more than an order of magnitude reduction in (transient) simulation time, by going from
a transistor-level circuit description to a macro-model for use with the same circuit
simulator.
All this does certainly not imply that one can now easily and quickly solve any modelling
problem by just throwing in some measurement or simulation data. Some behaviour is beyond
the representational bounds of our present feedforward neural networks, as has been addressed
in section 2.6. It is not yet entirely clear in which cases, or to what extent, feedback in dynamic
neural networks will be required in practice for device and subcircuit modelling. It has been
shown, however, that the introduction of external feedback to our dynamic neural networks
would allow for the representation, up to arbitrary accuracy, of a very general class of
nonlinear multidimensional implicit differential equations, covering any state equations of
the form f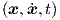 = 0 as used to express the general time evolution of electronic
circuits. It even makes these neural networks “universal approximators” for arbitrary
continuous nonlinear multidimensional dynamic behaviour. This will then also include, for
instance, multiple dc solutions (for modelling hysteresis and latch-up) and chaotic
behaviour.
= 0 as used to express the general time evolution of electronic
circuits. It even makes these neural networks “universal approximators” for arbitrary
continuous nonlinear multidimensional dynamic behaviour. This will then also include, for
instance, multiple dc solutions (for modelling hysteresis and latch-up) and chaotic
behaviour.
Still, it seems fair to say that many issues in nonlinear multidimensional dynamic modelling are only
beginning to be understood, and more obstacles are likely to emerge as experience accumulates.
Slow learning can in some cases be a big problem, causing long learning times in finding a (local)
minimum.
Since we are typically dealing with high-dimensional systems, having on the order of tens or
hundreds of parameters (= dimensions), gaining even a qualitative understanding of what is
going on during learning can be daunting. And yet this is absolutely necessary to know and
decide what fundamental changes are required to further improve the optimization
schemes.
In spite of the above reasons for caution, the general direction in automatic modelling as
proposed in this thesis seems to have significant potential. However, it must at the
same time be emphasized that there may still be a long way to go from encouraging
preliminary results to practically useful results with most of the real-life analogue
applications.
5.2 Recommendations for Further Research
A practical stumbling block for neural network applications is still formed by the often long
learning times for neural networks, in spite of the use of fairly powerful optimization techniques
like variations of the classic conjugate-gradient optimization technique, the use of several scaling
techniques and the application of suitable constraints on the dynamic behaviour.
This often appears to be a bigger problem than ending up with a relatively poor
local minimum. Consequently, a deeper insight into the origins of slow optimization
convergence would be most valuable. This insight may be gained from a further thorough
analysis of small problems, even academic “toy” problems. The curse of dimensionality
is here that our human ability to visualize what is going on fails beyond just a few
dimensions. Slow learning is a complaint regularly found in the literature of neural network
applications, so it seems not just specific to our new extensions for dynamic neural
networks.
A number of statistical measures to enhance confidence in the quality of models have not been
discussed in this thesis. In particular in cases with few data points as compared to the
number of model parameters, cross-validation should be applied to reduce the danger of
overfitting. However, more research is needed to find better ways to specify what a
near-minimum but still “representative” training set for a given nonlinear dynamic
system should be. At present, this specification is often rather ad hoc, based on a
mixture of intuition, common sense and a priori knowledge, having only cross-validation
as a way to afterwards check, to some unknown extent, the validity of the choices
made.
Various forms of residue analysis and cross-correlation may also be useful in the analysis of
nonlinear dynamic systems and models.
Related to the limitations of an optimization approach to learning is the need for more
“constructive” algorithms for mapping a target behaviour onto neural networks by using a priori
knowledge or assumptions. For combinatorial logic in the sp-form the selection of a topology
and a parameter set of an equivalent feedforward neural network can be done in a
learning-free and efficient manner—the details of which have not been included in
this thesis. However, for the more relevant general classes of analogue behaviour,
virtually no fast schemes are available that go beyond simple linear regression. On the
other hand, even if such schemes cannot by themselves capture the full richness of
analogue behaviour, they may still serve a useful role in a pre-processing phase to
quickly get a rough first approximation of the target behaviour. In other words, a
more sophisticated pre-processing of the target data may yield a much better starting
point for learning by optimization, thereby also increasing the probability of finding a
good approximation of the data during subsequent learning. Pole-zero analysis, in
combination with the neural network pole-zero mapping as outlined in section 2.4.2, could
play an important role by first finding a linear approximation to dynamical system
behaviour.
Another important item that deserves more attention in the future is the issue of dynamic
neural networks with feedback. The significant theoretical advantage of having a “universal
approximator” for dynamic systems will have to weighed against the disadvantages of giving up
on explicit expressions for behaviour and on guarantees for uniqueness of behaviour, stability
and static monotonicity. In cases where feedback is not needed, it clearly remains
advantageous to make use of the techniques as worked out in detail in this thesis, because it
offers much greater control over the various kinds of behaviour that one wants or
allows a dynamic neural network to learn. Seen from this viewpoint, it can be stated
that the approach as presented in this thesis offers the advantage that one can in
relatively small steps trade off relevant mathematical guarantees against representational
power.
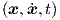 = 0 as used to express the general time evolution of electronic
circuits. It even makes these neural networks “universal approximators” for arbitrary
continuous nonlinear multidimensional dynamic behaviour. This will then also include, for
instance, multiple dc solutions (for modelling hysteresis and latch-up) and chaotic
behaviour.
= 0 as used to express the general time evolution of electronic
circuits. It even makes these neural networks “universal approximators” for arbitrary
continuous nonlinear multidimensional dynamic behaviour. This will then also include, for
instance, multiple dc solutions (for modelling hysteresis and latch-up) and chaotic
behaviour.